Method for constructing regular LDPC codes with larger girth
Gallager proposed Low Density Parity Check (LDPC) code in 1962, and later Tanner made a valuable addition to it, until it was re-proposed by Mackey in 1995. If the sum product iterative decoding algorithm is used, the LDPC code has a performance very close to the Shannon limit. If there is a loop in the Tanner graph of the LDPC code, the error information will expand during the iterative decoding process, which is very harmful to the decoding performance of the LDPC, especially the existence of shorter loops, and the harm is particularly serious. Therefore, in the process of constructing LDPC, it is necessary to avoid the appearance of short loops. In order to minimize the impact of the existence of the ring in the Tanner graph on the performance of the corresponding LDPC code under the sum product decoding algorithm, some research scholars have proposed some LDPC code construction methods with larger girths based on algebraic methods and heuristic search methods . Research shows that by increasing the girth of the LDPC code, the error correction performance of the code can be improved to a certain extent. In this paper, a regular LDPC code is constructed. During the construction process, the parameter selection of the design girth is discussed, so that certain conditions can be met to avoid the small girth of the check matrix, and the constructed matrix has a larger girth.
1. Construction theory of LDPC codes
Consider the Tanner corresponding to the (2, 4) regular LDPC code of length 16, as shown in Figure 1. 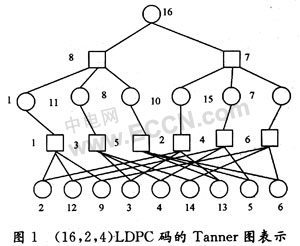
It can be clearly seen from FIG. 1 that the minimum length of the Tanner ring is 8, so the girth of the corresponding LDPC code is also 8.
Number the variable nodes and check nodes in sequence according to Figure 1 to obtain the check matrix corresponding to the LDPC code, as shown in Figure 2. 
The matrix in Fig. 2 is very regular, and can be seen as the splicing of two cyclic square matrices with a row weight of 2 and a dimension of 8 × 8. Therefore, it can be guessed that some regular matrices are combined into a check matrix, so that the generated LDPC code is likely to have a larger girth. In other words, by splitting the check matrix of the LDPC code into several sub-matrices, and then constructing each sub-matrix according to a certain rule, it is possible to avoid the appearance of small loops.
The idea of ​​matrix splitting is adopted here. Let us construct a (λ, Ï) regular LDPC code with a length of 72 (n = ÏUU∈N), and split the check matrix of the code into (λ, Ï) U × U sub-matrices. 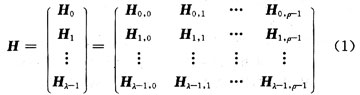
In the formula: each sub-matrix Hi, j = I (ai, j) (0≤i <λ, 0≤j <Ï) is a unit matrix or the cyclic shift of the unit matrix ai, j represents each row of the unit matrix The number of digits to rotate right. Obviously, the check matrix constructed in this way cannot be full rank, at most λÏ-λ-1.
For ease of description, A = (ai, j) is used to denote the matrix composed of the cyclic shift parameters of each sub-matrix, and (I, J, i, j) is used to denote the elements in the check matrix, where (I, J ) Is the coordinate of the sub-matrix to which the element belongs, (i, j) is the coordinate of the element in the sub-matrix to which it belongs. The minimum length of all the loops in which each variable node participates in the Tanner graph is the loop length of the variable node. Obviously, the girth of the corresponding LDPC code is equal to the minimum loop length of each variable node. The n variable nodes are divided into P groups, and each group of variable nodes corresponds to a list of sub-matrices. Considering the cyclic characteristics of each sub-matrix, the following theorem holds.
Theorem 1 Variable nodes belonging to the same group have the same ring length.
Proof: Assume that any two variable nodes x and y of the same group correspond to the x and y columns of a sub-matrix, respectively, and yx = dmodU, the ring lengths are C (x) and C (y) The minimum loop path of the variable node x is shown in Figure 3. 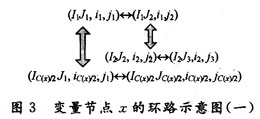
According to the cyclic characteristics of each sub-matrix, the path of another ring can be found as shown in Fig. 4. 
Obviously the loop length is C (x) and passes through the variable node y, so there are:
C (x) ≥C (y) (2)
Similarly, we can get:
C (x) ≤C (y) (3)
Combining the above two formulas, C (x) = C (y) means that for any two variable nodes of the same group, their ring lengths are equal, and the proof is completed.
It can be seen from Theorem 1 that for the LDPC code corresponding to the check matrix constructed according to the above method, the loop lengths of all variable nodes have at most Ï types, so for a matrix constructed in this way, only one variable node needs to be extracted from each group, and then Only by detecting the Ï variable nodes, the girth of the entire code can be determined.
2 Selection of cyclic shift parameters in the check matrix
The case of 4 rings is discussed below. If an LDPC code contains 4 loops, then there must be 4 "1s" in the check matrix corresponding to the four vertices of a rectangle. The loop path can be expressed as: 
Theorem 2 The sufficient and necessary conditions for the LDPC code corresponding to the matrix constructed according to the matrix splitting method shown in equation (1) without the ring of length 4 are satisfied by equation (6): 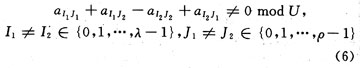
The correctness of this theorem can be known from the previous description, and will not be repeated here.
Theorem 2 is easy to get the following inference:
Corollary 1: The sufficient and necessary conditions for the LDPC code corresponding to the matrix constructed according to the matrix splitting construction method shown in equation (1) without the ring of length 2l are: 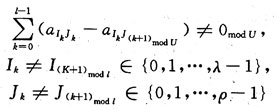
In coding design, you can first determine the design girth of the constructed LDPC code, then list the corresponding unequal constraints according to the above theorem and inference, and then find the parameters that meet these unequal constraints.
When choosing parameters, you can list the constraint equations corresponding to each parameter according to the girths analyzed and designed above, and then find the values ​​of the parameters that satisfy these constraint equations. However, since these constraint equations are all unequal constraints, the general method of solving equations cannot be used; if an exhaustive method is used to traverse all possible combinations of various parameters, and then find a set that meets the constraints, the search range There will be U (λ-1) (Ï-1), so even if the value range of U is very small (such as 102), the total search range will also be very large, so it cannot be achieved.
In order to realize the rapid selection of parameters, the following parameter-by-parameter trial algorithm can be used:
(1) Let ai, 0 = 0 (i = 0,1, ..., λ-1) and a0, j = 0 (j = 1,2, ..., Ï-1);
(2) Randomly choose the value of a1,1 in {0,1, ..., U-1), and then judge whether a1,1 satisfies the given unequal constraints, if it is satisfied, determine the value, otherwise re-execute (2 )
(3) Determine the cyclic shift parameters of the remaining sub-matrix at once according to the method of (2).
According to the above algorithm, each parameter requires at most U trials, so that the total number of trials is at most (λ-1) (Ï-1) U, which is much smaller than the entire search space U (λ-1) (Ï-1).
Since the algorithm adopts the method of determining the parameters one by one, it is obvious that the final parameter is subject to the most constraints. Define N (l) to consider the number of constraint equations that the last parameter is subjected to when eliminating the loop of length 2l in the Tanner graph, then Have: 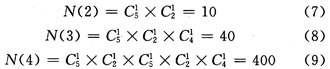
Since each constraint equation is an unequal constraint, each constraint can only limit the parameter to a certain value, so the number of values ​​that all the unequal constraint limit parameters cannot take is at most twice the number of constraint equations. Considering the code length of the LDPC code to be constructed, the value of U is generally around 100, so it is generally feasible to eliminate the six loops.
3 Simulation and performance analysis
Take U = 168, construct the (3, 6) regular LDPC code with a length of 1 008 according to the above method, and find it through computer search and detection, and get the loop parameters of the sub-square matrix as:
The detection found that the girth of the LDPC code is 10, in order to ensure that the code rate of the constructed code is strictly equal to 0.5, two "1" s can be deleted from the generated check matrix. The error correction performance of the code under the AWGN channel is shown in Figure 5. The other two curves in the figure are the performance curves of the same length, random structure, and (4, 3) regular LDPC codes without eliminating 4 loops. Among them, girth represents the girth; ave represents the average ring length of all variable nodes.
The literature [8, 9] uses the PEG algorithm to construct a (3, 6) regular LDPC code with a length of 1,008 and a girth of 8, with an average ring length of 9.66, which is slightly inferior to the LDPC code constructed above, so this method is used The construction of regular LDPC codes is superior to other construction methods.
Through analysis, it is found that the regular LDPC code constructed by this method is the same as the method described in [10], and its girth has an upper limit, which will be described in detail below. Consider a matrix with a dimension of 2U × 3U, and split it into 6 sub-square matrices with a dimension of U × U. Each square matrix is ​​a unit matrix or a row cyclic shift of the unit matrix. A matrix with a weight of 3 and a column weight of 2. Without loss of generality, the sub-arrays in the first row are unit arrays, and the right-circular shift parameters of the other two square arrays are a1, 1 and a1,2, no matter how a1, 1 and a1, 3 are taken. Value, the matrix always has 12 rings as shown in Figure 6. 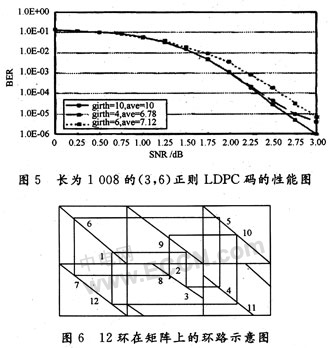
Number the non-zero elements on the ring in Fig. 6 in sequence, and let the coordinate of the element with the number 1 be (0, 0, x, x), then the coordinates of the nodes on the ring are shown in Fig. 7. 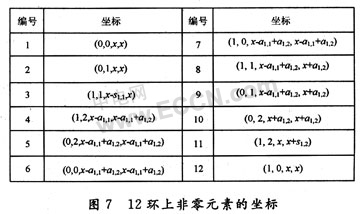
Therefore, if the above method is used to construct the (λ, Ï) regular LDPC code, as long as λ ≥ 2, Ï â‰¥ 2 and λ + Ï â‰¥ 5, the corresponding check matrix must also include the word matrix shown in the figure or its Transpose the matrix, so the girth of the obtained LDPC code is inevitably impossible to exceed 12.
4 Conclusion
A high-girth regular LDPC code construction method is given, and the delooping method and the selection of cyclic shift parameters are specifically analyzed. The H matrix of the LDPC code constructed in this way has a very good structure. Simulation shows that the code constructed by this method performs better than the randomly constructed code under AWGN channel.
Oil-immersed Distribution Transformer, its HV level is 20kV, LV is 400V, its capacity is 2500kVA and below. Generally installed on the pole or in the distribution room, for lighting or power supply, three-phase power supply, fully sealed tank structure, to ensure the transformer safe and reliable operation.
20Kv Transformer,20Kv Distribution Transformer,20Kv Oil Immersed Transformer,High Quality 20Kv Transformer
Hangzhou Qiantang River Electric Group Co., Ltd.(QRE) , https://www.qretransformer.com